FAQs About Water and Steam
While IAPWS is not an educational organization, we occasionally get questions from students and others seeking basic scientific information about water and steam and their uses. While we are not equipped to answer such questions individually, we have decided to collect answers to some of the most common questions in the hope that we can meet the needs of many of the people who come across this website looking for general information about water.
If you do not find the answer to the question you are looking for, we can point you to some additional resources.
If you are looking for information specifically about the structure and activities of IAPWS, try our page of FAQs about IAPWS.
Because water is commonly available in fairly pure form, it has historically been used as a reproducible standard for defining physical quantities. Most of those old standards using water have been superseded by more precise standards. However, it is still interesting and instructive to trace the ways in which water has been used as a measurement standard.
Probably the most familiar such use of water is in connection to the temperature scale. The Celsius (sometimes called Centigrade, though use of that term is no longer considered correct) temperature scale was originally defined so that the freezing point and boiling point of pure water, both at one atmosphere pressure, were 0 and 100 degrees, respectively. This definition ceased to be valid with the adoption of a new International Temperature Scale in 1990.
The thermodynamic definition of temperature is based solely on the behavior of an ideal gas; also one fixed point is needed to set the size of the degree. The fixed point used is the "triple point" of water, which is the pressure/temperature condition where solid, liquid, and vapor all coexist. This is used because the triple point is a unique condition that can be precisely reproduced; water's triple point is specifically chosen because it is relatively convenient to realize in the laboratory.
The thermodynamic temperature of the triple point of water was defined for many years to be exactly 273.16 kelvins (where 0 K is the absolute zero of temperature). In 2018, the definition of the kelvin was changed to refer to a fixed value of the Boltzmann constant, but the best estimate of the triple point of water is still 273.16 K.
While this completely determines the thermodynamic temperature scale, temperature measurements require approximating the thermodynamic temperature by a "practical" scale that contains many fixed points at which instruments can be calibrated. Temperatures are assigned to these points based on the best scientific estimate of their true thermodynamic temperatures, and procedures are specified for interpolating between the fixed points. While previous temperature scales used the atmospheric boiling point of water as a fixed point (assigning it 373.15 K, which is 100 degrees Celsius), the reproducibility of that point is not as good as other choices. The current International Temperature Scale adopted in 1990 (known as ITS-90) covers this region with the solid/liquid equilibrium (melting/freezing) points of gallium (302.9146 K) and indium (429.7485 K). On ITS-90, the atmospheric boiling temperature of water turns out to be approximately 373.124 K (99.974 degrees Celsius). [Another important fixed point of ITS-90 is the triple point of water, which is exactly 273.16 K on that scale.]
So, have the properties of water changed? Of course not. What has changed is our ability to precisely determine temperatures in closer approximation to the true thermodynamic temperature. It turns out that the true temperature of water's boiling point is not quite what people thought it was when the Celsius scale was first defined long ago.
It is sometimes asked why one could not redefine the temperature scale so that the familiar 0 and 100 degrees Celsius would still hold for the freezing and boiling points of water. This could be done, but it would require changing the size of the degree; this would distort another familiar relationship because the difference between absolute temperature in kelvins and the Celsius scale would have to become approximately 273.22 rather than the familiar 273.15. Also, such a definition would require changing the whole scale if more accurate measurements were ever made for water's boiling point. It is better to base temperature on fundamental physics (in this case, the laws of thermodynamics applied to an ideal gas) and use a precisely reproducible point (such as water's triple point) to define the scale. Of course for most practical uses, it is an adequate approximation to think of water as boiling at 100 degrees Celsius rather than 99.974.
The other important historical use of water as a measurement standard has been in the definition of mass. The gram was originally defined as the mass of one cubic centimeter of water at some standard condition. Many years ago, the mass standard was changed to the standard kilogram, a platinum/iridium cylinder kept in Paris. In 2018, the dependence on a physical artifact was eliminated, and the kilogram is now defined solely in terms of defined values of fundamental physical constants such as the Planck constant. Careful measurements have shown that liquid water at its density maximum has a density slightly less than 1 g/cm3; the currently accepted number is 0.999975 g/cm3.
For more on the fundamental definitions of SI units, see this website of the BIPM.
A microwave oven heats water because the microwave radiation interacts with the dipole (separated positive and negative charge) of the water molecule. The microwaves turn the water molecules back and forth at approximately the frequency of the microwaves, imparting energy to them. Sometimes you may hear that the microwaves are interacting with a resonant frequency of the water molecule (like a radio gets tuned to a frequency), but that is actually not the case. Anything with a dipole moment will absorb microwave radiation, so microwave ovens will also heat fats and sugars, for example.
A fairly simple explantion of how a microwave oven works is at this website.
As for the second part of the question, there is indeed some danger of sudden boiling of water that has been microwaved. The reason is that it is possible for water to get "superheated." Normally, we think of water boiling when it reaches its boiling temperature. But, boiling doesn't start until there is "nucleation" of bubbles - some irregularity to get the process started. If there is no nucleation, the liquid can be heated above its boiling point (this is called being "superheated"). A similar phenomenon can result in cooling below the freezing point; this state is called "supercooled."
Superheated water can be dangerous. As soon as nucleation occurs (perhaps by putting something in the water or moving the container), all the stored energy which was used to heat the water above its boiling temperature will go into boiling the liquid. This sudden large amount of boiling can produce scalding if you are too close to it.
We have included this second part of the question because it comes up often, especially in the form of a story that has been widely circulated on the Internet. The story tells of an unfortunate person who heated water in a microwave, took it out and looked into the cup, and had the water "blow up" in sudden violent boiling and scald his face horribly. The recipient of the e-mail is urged to forward the warning "to friends and family."
Many stories like this that get passed around the Internet are hoaxes (especially the ones that ask to be forwarded to everyone you know). While this particular e-mail may well be such a hoax, and is probably overly alarmist, the potential problem it warns about is real. The possible "Urban Legend" nature of the specific story that circulates on the Internet is discussed on these Websites:
Please note again (as both of these sites mention) that there is a real danger, because of the possibility of superheating the water.
The U.S. Food and Drug Administration has a page with safety information about microwave ovens:
All liquids, at any temperature, exert a certain vapor pressure. The vapor pressure can be thought of as the degree to which the liquid molecules are escaping into the vapor phase. The vapor pressure increases with temperature, because at higher temperature the molecules are moving faster and more able to overcome the attractive intermolecular forces that tend to bind them together. Boiling occurs when the vapor pressure reaches or exceeds the surrounding pressure from the atmosphere or whatever else is in contact with the liquid.
At standard atmospheric pressure (1 atmosphere = 0.101325 MPa), water boils at approximately 100 degrees Celsius. That is simply another way of saying that the vapor pressure of water at that temperature is 1 atmosphere. At higher pressures (such as the pressure generated in a pressure cooker), the temperature must be higher before the vapor pressure reaches the surrounding pressure, so water under pressure boils at a higher temperature. Similarly, when the surrounding pressure is lower (such as at high altitudes), the vapor pressure reaches that pressure at a lower temperature. For example, in the Denver, Colorado area of the U.S. where the elevation above sea level is approximately one mile (1600 meters), the atmospheric pressure is about 83% of a standard atmosphere, and water boils at approximately 95 degrees Celsius.
The relationship between vapor pressure and temperature (or, looked at in the reverse direction, between boiling temperature and pressure) is called the vapor pressure curve. Water's vapor pressure curve is of great importance, since it determines the relationship between temperature and pressure in any process where water is going from a liquid to a vapor state or vice-versa. Such processes are important both in industry (for example in steam power generation where water is made into steam in boilers and eventually condensed after running through turbines) and in nature (for example, in rainfall and evaporation from bodies of water).
In the following table, we list the vapor pressure for water as a function of temperature as taken from the latest IAPWS formulation for general and scientific use.
| Temperature (degrees Celsius) |
Vapor Pressure (MPa) |
|---|---|
| 0.01 | 0.000 612 |
| 25 | 0.003 17 |
| 50 | 0.012 35 |
| 75 | 0.0386 |
| 100 | 0.1014 |
| 150 | 0.4762 |
| 200 | 1.555 |
| 250 | 3.976 |
| 300 | 8.588 |
| 350 | 16.529 |
| 373.946 | 22.064 |
The first value in the table is for water's triple point, which is the thermodynamic state where vapor, liquid, and solid coexist. The last value is for water's critical point. The critical point is the end of the vapor pressure curve; there the vapor and liquid phases become identical and at higher temperatures there is only a single fluid phase.
Water is made of hydrogen and oxygen, but both of these elements have more than one stable naturally occurring isotope. The most abundant hydrogen isotope has an atomic mass number of 1, but the mass number of 2 (called deuterium and often represented by the symbol D) is present in small quantities. Tritium (mass number 3, often represented by the symbol T) is radioactive and is almost entirely absent in nature. The most abundant oxygen isotope has a mass number of 16, but the 18-O isotope is present at about 0.2% and there is also a tiny amount of 17-O.
The isotopic composition of water (like other chemical compounds) is not uniform. This is because some chemical reactions discriminate between isotopes and because of differences in volatility between compounds made with different isotopes. It is this last effect that is most noticeable for water. When water vaporizes, the vapor is slightly depleted in the heavier isotopes. The opposite occurs when water condenses from the atmosphere; the rain or snow has more of the heavy isotopes, leaving lighter water vapor in the atmosphere. These phenomena are important to those who study the climate, because isotopic compositions can be used to trace the global flows of water and other compounds.
Because of these effects, fresh waters on Earth vary relatively widely in their isotopic composition. In temperate climates, fresh water is about 4% depleted in deuterium compared to ocean water. In the polar regions, this depletion can reach 40%.
Despite this variation, it is important to have a "standard" water which is easily reproducible and against which other waters can be compared. Fortunately, ocean water can provide such a standard. The isotopic composition of deep offshore ocean water is remarkably uniform across the Earth. This has been used to create a standard called Vienna Standard Mean Ocean Water (VSMOW). VSMOW is the standard against which isotopic compositions of both hydrogen and oxygen are reported. The isotopic composition of VSMOW and related information are documented in this report.
"Standard" values for water properties, including formulations produced by IAPWS, are considered to be for VSMOW. For the most precise scientific work, it may be necessary to convert some values between VSMOW and the water actually used (for example, the difference in density due to isotopic composition between VSMOW and purified tap water can be a few parts per million). The isotopic composition is also important in converting between mass-based and molar units; the relative molar mass of VSMOW is 18.015268 g/mol.
Finally, we can mention "heavy water." Heavy water is normally defined as water where the hydrogen is 100% deuterium, but the oxygen has the isotopic composition of VSMOW. The relative molar mass of heavy water by this definition is 20.027508 g/mol.
A water molecule consists of two hydrogen atoms and one oxygen atom. The three atoms make an angle; the H-O-H angle is approximately 104.5 degrees. The center of each hydrogen atom is approximately 0.0957 nm from the center of the oxygen atom. The structure of a single water molecule is shown below:
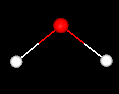
The pictures on this page are provided courtesy of the MathMol project at the NYU/ACF Scientific Visualization Laboratory.
Information about MathMol can be found here.
Because oxygen is more electronegative than hydrogen (in other words, electrons tend to be in the neighborhood of the oxygen), the hydrogen atoms end up with a partial positive charge and the oxygen atom with a partial negative charge. This separation of charge produces a net dipole moment on the molecule; for the isolated water molecule this dipole moment is approximately 1.85 Debye units.
This molecular structure leads to hydrogen bonding, which is a stabilized structure in which a hydrogen atom is in a line between the oxygen atom on its own molecule and the oxygen on another molecule. This picture shows a hydrogen-bonded structure between two water molecules:
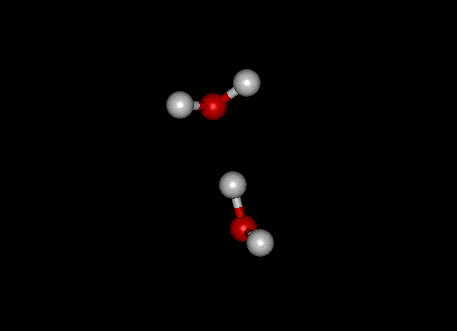
These hydrogen bonds, with their extra attractive energy, are the cause of many of the unusual properties of water, including its large heat of vaporization and its expansion upon freezing.
Most liquids have a quite simple behavior when they are cooled (at a fixed pressure): they shrink. The liquid contracts as it is cooled; because the molecules are moving slower they are less able to overcome the attractive intermolecular forces drawing them closer to each other. Then the freezing temperature is reached, and the substance solidifies, which causes it to contract some more because crystalline solids are usually tightly packed.
Water is one of the few exceptions to this behavior. When liquid water is cooled, it contracts like one would expect until a temperature of approximately 4 degrees Celsius is reached. After that, it expands slightly until it reaches the freezing point, and then when it freezes it expands by approximately 9%.
This unusual behavior has its origin in the structure of the water molecule. There is a strong tendency to form a network of hydrogen bonds, where each hydrogen atom is in a line between two oxygen atoms. This hydrogen bonding tendency gets stronger as the temperature gets lower (because there is less thermal energy to shake the hydrogen bonds out of position). The ice structure is completely hydrogen bonded, and these bonds force the crystalline structure to be very "open", as shown in the following picture:
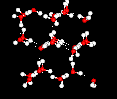
The pictures on this page are provided courtesy of the MathMol project at the NYU/ACF Scientific Visualization Laboratory.
Information about MathMol can be found here.
In the following two pictures, the first shows a typical structure of liquid water, while the second is an ice structure; note the extra open space in the ice.

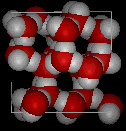
It is this open solid structure that causes ice to be less dense than liquid water. That is why ice floats on water, for which we should all be thankful because if water behaved "normally" many bodies of water would freeze solid in the winter, killing all the life within them.
Water's "density maximum" is a product of the same phenomenon. Close to the freezing point, the water molecules start to arrange locally into ice-like structures. This creates some "openness" in the liquid water, which tends to decrease its density. This is opposed by the normal tendency for cooling to increase the density; it is at approximately 4 degrees Celsius that these opposing tendencies are balanced, producing the density maximum.
All liquids, at any temperature, exert a certain vapor pressure. The vapor pressure can be thought of as the degree to which the liquid molecules are escaping into the vapor phase. The vapor pressure increases with temperature, because at higher temperature the molecules are moving faster and more able to overcome the attractive intermolecular forces that tend to bind them together. Boiling occurs when the vapor pressure reaches or exceeds the surrounding pressure from the atmosphere or whatever else is in contact with the liquid.
At standard atmospheric pressure (1 atmosphere = 0.101325 MPa), water boils at approximately 100 degrees Celsius. That is simply another way of saying that the vapor pressure of water at that temperature is 1 atmosphere. At higher pressures (such as the pressure generated in a pressure cooker), the temperature must be higher before the vapor pressure reaches the surrounding pressure, so water under pressure boils at a higher temperature. Similarly, when the surrounding pressure is lower (such as at high altitudes), the vapor pressure reaches that pressure at a lower temperature. For example, in the Denver, Colorado area of the U.S. where the elevation above sea level is approximately one mile (1600 meters), the atmospheric pressure is about 83% of a standard atmosphere, and water boils at approximately 95 degrees Celsius.
The relationship between vapor pressure and temperature (or, looked at in the reverse direction, between boiling temperature and pressure) is called the vapor pressure curve. Water's vapor pressure curve is of great importance, since it determines the relationship between temperature and pressure in any process where water is going from a liquid to a vapor state or vice-versa. Such processes are important both in industry (for example in steam power generation where water is made into steam in boilers and eventually condensed after running through turbines) and in nature (for example, in rainfall and evaporation from bodies of water).
In the following table, we list the vapor pressure for water as a function of temperature as taken from the latest IAPWS formulation for general and scientific use.
| Temperature (degrees Celsius) |
Vapor Pressure (MPa) |
|---|---|
| 0.01 | 0.000 612 |
| 25 | 0.003 17 |
| 50 | 0.012 35 |
| 75 | 0.0386 |
| 100 | 0.1014 |
| 150 | 0.4762 |
| 200 | 1.555 |
| 250 | 3.976 |
| 300 | 8.588 |
| 350 | 16.529 |
| 373.946 | 22.064 |
The first value in the table is for water's triple point, which is the thermodynamic state where vapor, liquid, and solid coexist. The last value is for water's critical point. The critical point is the end of the vapor pressure curve; there the vapor and liquid phases become identical and at higher temperatures there is only a single fluid phase.
Most liquids have a quite simple behavior when they are cooled (at a fixed pressure): they shrink. The liquid contracts as it is cooled; because the molecules are moving slower they are less able to overcome the attractive intermolecular forces drawing them closer to each other. Then the freezing temperature is reached, and the substance solidifies, which causes it to contract some more because crystalline solids are usually tightly packed.
Water is one of the few exceptions to this behavior. When liquid water is cooled, it contracts like one would expect until a temperature of approximately 4 degrees Celsius is reached. After that, it expands slightly until it reaches the freezing point, and then when it freezes it expands by approximately 9%.
This unusual behavior has its origin in the structure of the water molecule. There is a strong tendency to form a network of hydrogen bonds, where each hydrogen atom is in a line between two oxygen atoms. This hydrogen bonding tendency gets stronger as the temperature gets lower (because there is less thermal energy to shake the hydrogen bonds out of position). The ice structure is completely hydrogen bonded, and these bonds force the crystalline structure to be very "open", as shown in the following picture:

The pictures on this page are provided courtesy of the MathMol project at the NYU/ACF Scientific Visualization Laboratory.
Information about MathMol can be found here.
In the following two pictures, the first shows a typical structure of liquid water, while the second is an ice structure; note the extra open space in the ice.


It is this open solid structure that causes ice to be less dense than liquid water. That is why ice floats on water, for which we should all be thankful because if water behaved "normally" many bodies of water would freeze solid in the winter, killing all the life within them.
Water's "density maximum" is a product of the same phenomenon. Close to the freezing point, the water molecules start to arrange locally into ice-like structures. This creates some "openness" in the liquid water, which tends to decrease its density. This is opposed by the normal tendency for cooling to increase the density; it is at approximately 4 degrees Celsius that these opposing tendencies are balanced, producing the density maximum.
The important word in that question is "specific". That means per unit of mass; the specific heat capacity would be the amount of energy that must be added to a unit mass to raise the temperature by one degree. But what really matters in determining thermodynamic properties is molecules, not mass. The heat capacity per molecule is related (to a first approximation) to the number of ways it can store energy (translational, vibrational, rotational). On a per molecule (or per mole) basis, water's heat capacity would be about the same as for other bent triatomic molecules (at a similar vapor or liquid condition) such as H2S. But because of the low molar mass of water (18), the *specific* heat capacity is larger. NH3 (molecular weight 17) has even a slightly higher *specific* heat capacity than water at similar conditions, again mainly because of the low molar mass.
So there is nothing really peculiar about the specific heat capacity of water. It is higher than most other liquids, but that is mainly because a given mass of water contains more molecules (and therefore more degrees of freedom in which to store energy) than the same mass of other liquids.
Books
Even in this age of the Web, the best way to learn about a subject (other than working in the subject area yourself) is to read a good book on it.
- One introductory-level book you might be able to find in a library is Water, by L.B. Leopold and K.S. Davis, a volume in the Life Science Library published by Time Inc. in 1966.
- A more recent book which looks at the role of water in many areas of science and society is Life's Matrix: A Biography of Water by Philip Ball (Farrar, Straus and Giroux, New York, 2000, first published in Great Britain in 1999 by Weidenfeld and Nicolson as H2O: A Biography of Water).
- A short book with a lot of scientific information on water (at about a college level) is Water by Felix Franks (Royal Society of Chemistry, London, 1983).
Websites
There are also some sources of information about water on the WWW:
- The U.S. Geological Survey has an extensive "Water Science School" (click here to go to website).
- For information on water as a natural resource, a project at the University of Minnesota has constructed a "Water on the Web" (click here to go to website)
- A 2023 review article describes the current state of knowledge of the thermophysical properties of water and heavy water. (click here to go to website)
- Finally, we can mention a website that is specifically devoted to answering scientific questions, primarily from students. It is called the Mad Scientists Network (click here to go to website). There you can search their collection of answers to common scientific questions, and if you don't find the answer you need you can submit your question to be answered by one of their network of experts.
Web design by Tribal Systems

